What Are the Different Types of Springs?

Springs are everywhere, from the tiny ones in your pen to the heavy-duty springs in your car. They come in all shapes and sizes, each designed for a specific job. If you've ever wondered about the different types of springs and how they make our everyday gadgets work, you're in the right place! In this guide, we'll dive into the world of compression, extension, torsion, and conical springs. We'll break down what makes each type unique, where they're used, and we’ll give you some cool design tips. Plus, we'll show you how to use some handy tools from Acxess Spring to take your spring projects to the next level. Whether you're a maker, manufacturer, inventor, or just curious, read on to learn all about these essential components!

Compression Springs

Compression springs are open-coil helical springs designed to resist a compressive force applied axially. These springs are commonly used to provide resistance to linear compressive forces and to store energy. Their design allows them to return to their original shape after being compressed, making them highly versatile and useful in numerous applications.

Characteristics

Compression springs are characterized by their helical shape, which can vary in pitch and diameter depending on the intended application. These springs are designed to resist compressive forces and store mechanical energy when compressed, returning to their original shape once the force is removed. They are typically made from durable materials such as music wire, or stainless steel, each offering different properties in terms of strength, corrosion resistance, and flexibility. The dimensions of compression springs, including wire diameter, outer diameter, inner diameter, free length, and solid height, can be adjusted to meet specific application requirements. The pitch, or distance between coils, and the number of active coils also play significant roles in determining the spring's characteristics. The spring rate, or spring constant, is a crucial parameter influenced by the wire diameter, coil diameter, and the number of active coils, determining how much force is required to compress the spring. This diverse range of characteristics makes compression springs highly versatile, with applications in automotive suspension systems, electronic devices, medical instruments, aerospace components, industrial machinery, and consumer products. Understanding these properties allows engineers to customize compression springs for optimal performance and reliability in their specific applications.

Applications

Compression springs are ubiquitous in various industries due to their versatility and efficiency.

• Automotive Industry: In the automotive industry, compression springs are essential components of suspension systems, helping to absorb shocks and maintain vehicle stability. They ensure a smoother ride by absorbing the impact from road irregularities, contributing to both passenger comfort and vehicle control. Additionally, they are used in engine valves, where they return the valve to its closed position after opening, maintaining engine timing and efficiency.

• Consumer Electronics: Consumer electronics, such as keyboards and battery contacts, rely on small compression springs to provide tactile feedback and secure connections. In keyboards, these springs are responsible for the "click" feel, enhancing the user experience by providing responsive feedback with each keystroke. In battery compartments, they ensure that batteries remain in contact with the terminals, providing a reliable power connection that is crucial for the device's operation.

• Medical Devices: In the medical field, compression springs are critical in various devices, including insulin pumps, inhalers, and surgical instruments. For instance, in insulin pumps, they are used to deliver precise doses of medication, ensuring consistent and accurate administration. Their reliability and precision are vital in maintaining patient health and safety.

• Aerospace: The aerospace industry utilizes compression springs in a variety of applications, from landing gear systems to control surfaces. These springs must withstand extreme conditions, including temperature variations and high stress, while maintaining their performance and reliability. They play a crucial role in ensuring the safety and functionality of aircraft components.

• Industrial Equipment: Industrial equipment, including valves and actuators, utilize compression springs to maintain consistent pressure and motion control. In valves, they help regulate the flow of liquids and gases by returning the valve to its closed or open position. In actuators, they assist in converting energy into mechanical motion, ensuring precise control over industrial processes.

• Home Appliances: In household appliances such as dishwashers, washing machines, and toasters, compression springs are used to control mechanisms and provide the necessary force to operate various components. For example, in toasters, they help eject the toast once it’s done, while in washing machines, they help absorb vibrations and maintain stability during the spin cycle.

• Toys and Gadgets: Compression springs are also widely used in toys and gadgets, providing motion and action. From simple wind-up toys to complex mechanical figures, these springs add functionality and entertainment value, making them essential components in the toy industry.

The widespread use of compression springs across these diverse applications underscores their importance in modern engineering and everyday life. Their ability to store and release energy, absorb shocks, and maintain force makes them indispensable in ensuring the functionality, safety, and efficiency of countless products and systems.

Formulas and Calculations

When designing compression springs, it's important to understand how stiff or flexible the spring will be under a given load. This property, known as the spring rate (k), can be determined using a specific formula. The formula incorporates key factors such as the material's rigidity, the wire diameter, the coil diameter, and the number of active coils. By applying the formula:

k = Gd^4 ÷ (8D^3 * n)

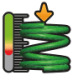
we can accurately calculate the spring rate, ensuring the spring will perform as expected within its mechanical system. This understanding is crucial for creating springs that balance strength and flexibility according to their intended application. We'll use the part number PC048-500-23500-MW-3000-C-N-IN as a reference to demonstrate key formulas in spring mechanics. This particular part will serve as our example to illustrate how to calculate spring rate and spring force. By referring to this stock spring part number, we can maintain clarity and coherence as we delve into these essential principles and their applications.

Where:

Step-by-Step Calculation

1. Calculate d^4: 

d^4 = (0.048)^4 = 0.048 × 0.048 × 0.048 × 0.048 = 0.000005308

2. Calculate D^3: 

D^3 = (0.452)^3 = 0.452 × 0.452 × 0.452 = 0.092356

3. Calculate 8 ⋅  D^3 ⋅ n: 

8 ⋅ D^3 ⋅ n = 8 × 0.092356 × 21.5 = 15.883

4. Calculate G ⋅ d^4: 

G ⋅ d^4 = 11492970.929 × 0.000005308 = 61.028

5. Calculate the spring rate k:

k = Gd^4 ÷ (8D^3 * n) = 61.028 ÷ 15.883 ​ = 3.84

So, the spring rate k is approximately 3.84 lbs/in

Hooke's Law is a principle of physics that states that the force needed to extend or compress a spring by some distance is proportional to that distance. The formula is given by:

F=k⋅x

Where:

• F is the force applied to the spring (in pounds or Newtons),

• k is the spring constant or spring rate (in pounds per inch or Newtons per meter),

• x is the displacement or travel of the spring from its equilibrium position (in inches or meters).

For this example, we need to calculate the force F required to compress a spring with a spring rate k of 3.841 lbs/in, as seen in the past example, by a distance x of 1.5 inches.

Substitute the values into Hooke's Law formula: 

F=k⋅x

Calculate the force: 

F = 3.841 lbs/in × 1.5 in

F = 5.7615lbs

The force required to compress the spring by 1.5 inches is approximately 5.7615 pounds. This calculation illustrates how Hooke's Law helps us understand the relationship between the force applied to a spring and the resulting displacement.

Case Study: Compression Spring Application in Precision Medical Devices

In the field of precision medical devices, small compression springs play a crucial role in ensuring reliable and consistent performance. One notable application is in the design of a compact insulin pump. The device requires a spring that can deliver precise doses of insulin with minimal variation. By utilizing a spring with a spring rate of 0.0334lbs/in, engineers were able to design a mechanism that ensures the accurate delivery of insulin, maintaining the required force to depress the pump mechanism without causing wear or fatigue over extended use. The small compression spring, made from high-grade stainless steel to resist corrosion and provide consistent performance, exemplifies how careful selection and calculation of spring parameters, including Hooke's Law for determining the force needed for operation, contribute to the overall success and reliability of critical medical devices. 

Extension Springs

Extension springs, also known as tension springs, are designed to operate with a tension load, meaning they stretch as the load is applied. These springs are used to provide a return force when extended and are often found in applications where components need to be held together or pulled back into position.

Characteristics

Extension springs are typically helical in shape with hooks, loops, or other forms of attachment at each end to connect to other components, allowing them to operate with a tension load by stretching as the load is applied. Made from materials such as spring steel, music wire, and stainless steel, these springs are chosen for their strength and elasticity, with each material offering unique properties such as high tensile strength, excellent fatigue resistance, and superior corrosion resistance. The design of extension springs includes various types of hooks or loops, such as machine hooks, cross-over center hooks, and side loops, to ensure secure attachment and efficient force transmission. Key dimensions like wire diameter, outer diameter, free length, and hook or loop length can vary to meet specific application requirements. The pitch and coil configuration, including uniform and variable pitch, along with the number of active coils, determine the spring's performance characteristics, with the spring rate being a crucial parameter influenced by these factors. Extension springs are widely used across various industries due to their ability to provide a controlled return force, making them essential indoor mechanisms, trampolines, medical devices, automotive systems, household appliances, toys, and industrial equipment. Their ability to store and release energy, provide controlled return forces, and maintain tension ensures the functionality, safety, and efficiency. 

Applications

Extension springs are widely used in various applications due to their ability to provide a controlled return force. Their versatility and functionality make them essential in numerous industries.

• Door Mechanisms: In door mechanisms, such as screen doors and garage doors, extension springs help to close the door smoothly and securely. For screen doors, they provide the necessary tension to ensure the door closes gently, preventing slamming and potential damage. In garage doors, extension springs counterbalance the weight of the door, making it easy to open and close while ensuring it stays securely in place when closed.

• Trampolines: Trampolines rely on extension springs to provide the necessary bounce and safety for users. These springs stretch and store energy when the trampoline mat is compressed, and then release that energy to propel the user upwards. The quality and strength of these springs are crucial for providing a consistent and safe jumping experience.

• Medical Devices: In the medical field, extension springs are used in various devices to ensure proper functionality and reliability. For instance, in fitness equipment such as resistance bands and physical therapy machines, extension springs provide the resistance needed for effective exercise and rehabilitation. Surgical instruments also utilize extension springs to return tools to their default position, ensuring precise and reliable performance during medical procedures.

• Automotive Industry: Extension springs are found in numerous automotive applications. They are used in vehicle suspension systems to absorb shocks and maintain vehicle stability. Additionally, they are employed in various components such as throttle return springs, which ensure the throttle closes when the driver releases the accelerator, and brake springs, which help to retract the brake shoes away from the drum.

• Appliances: Household appliances, such as vacuum cleaners and washing machines, utilize extension springs to control various functions. In vacuum cleaners, these springs help in retracting the power cord back into the device. In washing machines, they are used in the lid switch mechanisms, ensuring the machine stops operating when the lid is opened.

• Toys and Gadgets: Extension springs are commonly used in toys and gadgets, providing movement and action. From pull-back toy cars to mechanical wind-up toys, these springs add an element of fun and functionality. They store energy when pulled and release it to create motion, making them an integral part of many entertaining devices.

• Industrial Equipment: In industrial settings, extension springs are used in machinery and equipment to maintain tension and control movements. They are employed in conveyors, helping to maintain belt tension, and in levers and latches, ensuring secure and precise operation. Their ability to provide a controlled return force makes them valuable components in maintaining the efficiency and safety of industrial processes.

The widespread use of extension springs across these diverse applications highlights their importance in modern engineering and everyday life. Their ability to store and release energy, provide controlled return forces, and maintain tension ensures the functionality, safety, and efficiency of countless products and systems.

Formulas and Calculations

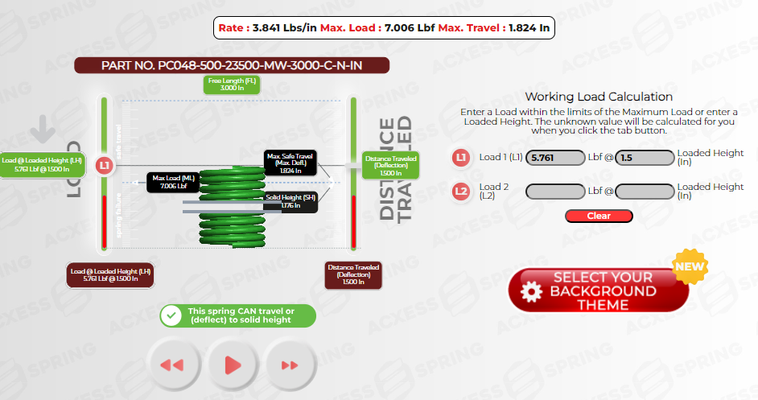
We'll be using the part number PE055-500-39364-MW-3000-CO-N-IN as our reference to illustrate how to calculate the spring force of an extension spring. By sticking with this stock spring part number, we can keep things clear and consistent as we dive into this essential concept and its application.

Hooke's Law states that the force exerted by a spring is directly proportional to the amount it is stretched or compressed, nd acts in the opposite direction. When an extension spring has initial tension, the total force required to extend the spring includes both the force due to initial tension and the force due to the spring rate. The formula is given by:

F = Initial Tension ​+ k ⋅ x

For this example, we need to calculate the total force F required to extend a 3 inches extension spring with an initial tension of 2.128 lbs and a spring rate k of 3.790 lbs/in to travel to a displacement x of 3 inches.

Substitute the values into the modified Hooke's Law formula: 

F = Initial Tension ​+ k ⋅ x

Calculate the force due to the spring rate: 

k ⋅ x = 3.790 lbs/in × 3 in = 11.370 lbs

Add the initial tension to the force due to the spring rate:

F = 2.128lbs + 11.370lbs = 13.498lbs

The total force required to extend the extension spring by 3 inches, considering the initial tension of 2.128 lbs and a spring rate of 3.790 lbs/in, is 13.498 pounds. This calculation demonstrates how both the initial tension and the spring rate contribute to the total force needed to extend the spring.

Case Study: Trampoline Springs

Trampolines rely heavily on the functionality and safety provided by extension springs. In designing a trampoline, high-quality extension springs made from stainless steel were chosen to address challenges such as durability, flexibility, and resistance to environmental factors like rust and corrosion. These springs, with a carefully calculated medium spring rate, ensure an optimal balance of strength and elasticity, providing the necessary bounce for users. The dimensions of the springs, including wire diameter, coil diameter, and the number of coils, were optimized for the expected load. Installed evenly around the trampoline's perimeter, the springs connect the mat to the steel frame using secure hooks. The implementation of these springs resulted in a significantly improved trampoline performance, offering users a consistent and enjoyable bounce. The stainless steel springs maintained their integrity and performance even after prolonged outdoor exposure. Future improvements may include enhanced corrosion resistance coatings and adjustable tension mechanisms to further extend the lifespan and versatility of the springs.

Torsion Springs

Torsion springs are designed to operate with a twisting motion. These springs store mechanical energy when twisted and release it when the twisting force is removed. They are commonly used in applications where rotational force is needed.

Characteristics

Torsion springs are typically helical with arms or legs extending from either end to attach to other components, designed to apply a rotational force or torque. Made from materials such as spring steel, music wire, and stainless steel, these springs are selected for their strength and flexibility. The spring rate, also known as the torsion spring constant, determines how much torque is required to twist the spring by a certain angle and is influenced by wire diameter, coil diameter, and the number of active coils. The arms or legs provide connection points and can be straight, hinged, or custom-shaped to fit specific requirements. Key dimensions like wire diameter, outer diameter, inner diameter, leg length, and the number of coils are crucial for their functionality. The pitch and coil configuration, whether uniform or variable, along with the number of active coils, affect the spring’s performance characteristics. Torsion springs are widely used in various applications due to their ability to provide controlled rotational force, making them essential in clothespins, mousetraps, automotive mechanisms, garage doors, industrial equipment, home appliances, toys, and medical devices. Their ability to store and release rotational energy, provide controlled movement, and maintain tension ensures the functionality, safety, and efficiency of countless products and systems.

Applications

Torsion springs are used in a variety of applications due to their ability to provide controlled rotational force. Their unique design and functionality make them essential in numerous industries and everyday devices.

• Clothespins: In clothespins, torsion springs provide the clamping force needed to hold clothes securely. The springs are coiled in the center, with the ends attached to the two halves of the clothespin. When the clothespin is squeezed, the torsion spring stores energy and then releases it to clamp down on the clothes, ensuring they stay in place on the clothesline.

• Mousetraps: Mousetraps use torsion springs to store and release energy quickly and effectively. When the trap is set, the torsion spring is under tension. Upon triggering, the spring releases its stored energy rapidly, causing the trap to snap shut with significant force. This quick and powerful action is essential for the mousetrap's effectiveness.

• Automotive Industry: In the automotive industry, torsion springs are used in various mechanisms to provide smooth and controlled motion. They are found in hood and trunk mechanisms, where they assist in the opening and closing process. Torsion springs provide the necessary force to lift the hood or trunk smoothly and hold it in the open position, preventing it from slamming shut. They are also used in car seat recliners and door hinges, ensuring controlled movement and stability.

• Garage Doors: Torsion springs are critical components in garage door systems. They are mounted above the door and wind and unwind as the door is opened and closed. The springs counterbalance the weight of the door, making it easier to lift manually or with an automatic opener. This reduces the strain on the garage door opener and ensures a smooth, controlled operation.

• Industrial Equipment: In industrial settings, torsion springs are used in machinery and equipment to provide controlled rotational force. They are employed in various applications such as conveyor belt tensioners, where they maintain consistent tension on the belt, and in levers and switches, ensuring precise and reliable operation.

• Home Appliances: Household appliances, such as dishwashers and washing machines, utilize torsion springs to control various functions. In dishwashers, torsion springs help in opening and closing the door smoothly, while in washing machines, they are used in the lid mechanisms to ensure the lid stays open or closed securely.

• Toys and Gadgets: Torsion springs are commonly used in toys and gadgets to provide movement and action. For instance, wind-up toys use torsion springs to store energy when wound up and release it to create motion. These springs add an element of fun and functionality, making them integral components in many entertaining devices.

• Medical Devices: In the medical field, torsion springs are used in various devices to ensure proper functionality and reliability. They are found in surgical instruments, where they provide the necessary force for precise control and operation. Torsion springs are also used in diagnostic equipment and patient care devices, where they contribute to the smooth and efficient performance of the equipment.

The widespread use of torsion springs across these diverse applications highlights their importance in modern engineering and everyday life. Their ability to store and release rotational energy, provide controlled movement, and maintain tension ensures the functionality, safety, and efficiency of countless products and systems.

Formulas and Calculations

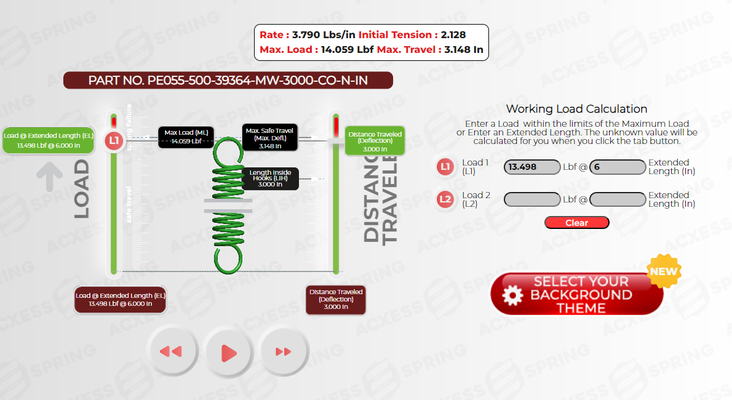
We'll use the part number PT015-183-3000-SST-LH-0510-N-IN as our example to demonstrate how to calculate the spring force of an extension spring. By referring to this stock spring part number, we can ensure clarity and coherence as we explore this fundamental concept and its practical application.

Hooke's Law states that the force exerted by a spring is directly proportional to the displacement from its equilibrium position. For torsion springs, this principle is applied to rotational displacement. The torque (rotational force) exerted by a torsion spring is proportional to the angle of twist from its neutral position. The formula is given by:

τ = k ⋅ θ

For this example, we need to calculate the torque τ exerted by a torsion spring with a spring rate k of 0.00066 in-lbs/deg when it is twisted to an angle θ of 90 degrees.

Substitute the values into the Hooke's Law formula for torsion springs: 

τ = k ⋅ θ

Calculate the torque: 

τ = 0.00066 in-lbs/deg × 90 deg = 0.0594in-lbs

The torque exerted by the torsion spring when twisted to 90 degrees is 0.0594 inch-pounds. This calculation illustrates how Hooke's Law is applied to torsion springs, showing the relationship between the spring rate, the angle of twist, and the resulting torque.

Case Study: Mouse Trap Mechanisms

Mousetraps are effective devices for rodent control, and the torsion spring is central to their operation, providing the necessary force to snap the trap shut quickly and efficiently. In designing an effective mousetrap, high-quality torsion springs made from music wire were selected for their high tensile strength and durability. These springs were designed with a specific torque to ensure a powerful snap while being easy to set. Installed around the trap's pivot point, the torsion springs stored energy when set and released it rapidly upon activation, causing the metal bar to snap down forcefully. Extensive testing confirmed that these springs delivered a quick and powerful snap, ensuring humane and effective rodent capture. The durability of the springs allowed for multiple uses without performance degradation, making them a reliable and cost-effective solution for rodent control. This case study highlights the importance of precision-engineered torsion springs in mousetrap mechanisms, ensuring their effectiveness and reliability through careful material selection and optimal design. Future improvements could include enhanced corrosion resistance and adjustable tension mechanisms to further optimize trap performance and user safety.

Conical Springs

Conical springs, also known as tapered springs, are designed to provide a near-constant spring rate and to allow the spring to compress to a solid height. These springs are often used in applications where space is limited, and a compact design is required.

Characteristics

Conical springs are characterized by their conical or tapered helical shape, which allows them to compress to a shorter height than cylindrical springs. They are made from materials such as spring steel, music wire, and stainless steel, chosen for their strength and flexibility. The spring rate varies along the length of the spring, providing a near-constant rate of resistance.

Applications

Conical springs are used in a variety of applications due to their compact design and consistent spring rate. Their unique shape, which allows for a variable pitch and a smaller compressed height, makes them ideal for numerous specialized uses across different industries.

• Aerospace Industry: In the aerospace industry, conical springs are used for vibration isolation. They provide reliable performance in demanding environments, absorbing and dampening vibrations to protect sensitive components and systems. Their ability to handle high stress and maintain consistent performance under extreme conditions makes them essential in aircraft and spacecraft applications.

• Electrical Contacts: Electrical contacts, such as battery terminals, rely on conical springs to maintain secure connections. These springs provide the necessary force to keep contacts in place, ensuring a stable and reliable electrical connection. Their compact design is especially useful in tight spaces where traditional springs may not fit, making them ideal for small electronic devices.

• Industrial Machinery: Industrial machinery utilizes conical springs for overload protection. These springs can absorb and dissipate energy when equipment experiences excessive loads, preventing damage and ensuring safe operation. Their ability to compress to a shorter height without sacrificing performance makes them suitable for applications where space is limited, but high load capacity is required.

• Automotive Industry: In the automotive industry, conical springs are used in various applications, such as suspension systems and valve mechanisms. Their ability to handle variable loads and provide a progressive spring rate makes them ideal for maintaining vehicle stability and performance. Additionally, their compact design allows for efficient use of space in crowded engine compartments.

• Medical Devices: Conical springs are employed in medical devices where compactness and precision are crucial. They are found in diagnostic equipment, where they help maintain consistent pressure and performance. In patient care devices, such as infusion pumps, conical springs ensure accurate dosing and reliable operation, contributing to patient safety and treatment efficacy.

• Consumer Electronics: In consumer electronics, conical springs are used in devices like remote controls and handheld gadgets. Their small size and reliable performance ensure that buttons and switches operate smoothly, providing a tactile response and maintaining the device's functionality over time. Conical springs also play a role in battery compartments, ensuring that batteries stay securely in place.

• Construction Equipment: Conical springs are used in construction equipment for shock absorption and load management. Their ability to compress to a minimal height while still providing strong support makes them ideal for heavy machinery and tools that experience variable loads and impacts. These springs help enhance the durability and performance of construction equipment.

• Toys and Gadgets: In toys and gadgets, conical springs provide motion and action in compact spaces. Wind-up toys, for example, use conical springs to store and release energy efficiently, enabling intricate movements in small mechanisms. Their versatility and reliable performance make them a popular choice for toy designers.

The widespread use of conical springs across these diverse applications highlights their importance in modern engineering and everyday life. Their compact design, consistent spring rate, and ability to handle high loads while maintaining a small compressed height ensure the functionality, safety, and efficiency of countless products and systems.

Formulas and Calculations

The spring rate of conical springs varies due to their unique geometry, making it complex to model accurately. However, a general approach to understanding their behavior involves considering the spring as a series of individual coils, each with its own spring constant. In this method, the spring is divided into segments, with each coil acting as a small spring. The overall spring rate is then determined by combining these individual rates, taking into account the varying diameters and lengths of each coil. This combination provides a near-constant rate of resistance throughout the compression process, despite the conical shape. By modeling the spring in this way, engineers can more accurately predict its performance and ensure it meets the specific requirements of its application. This approach allows for a more detailed analysis and design, ensuring that the conical spring provides consistent and reliable performance in a variety of settings.

Case Study: Aerospace Vibration Isolation

In the aerospace industry, protecting sensitive equipment from extreme vibrations and shocks is crucial. This case study explores the use of high-quality conical springs made from advanced stainless steel alloys in aerospace vibration isolation systems. These springs, designed with a variable pitch and smaller compressed height, offer excellent force absorption and damping capabilities while fitting within space and weight constraints. The advanced materials provide durability, high tensile strength, and corrosion resistance, ensuring consistent performance under extreme conditions. Extensive testing confirmed that these conical springs effectively protect sensitive instruments, maintaining their integrity and performance. Future enhancements may include advanced materials with greater temperature resistance and smart spring designs for real-time damping adaptation, further optimizing the reliability and efficacy of aerospace vibration isolation systems.

How to Improve your Spring Design?

From selecting the appropriate materials to optimizing the spring's dimensions and load-bearing capacity, engineers and designers must navigate a range of factors to create efficient and reliable springs. Here’s a closer look at some of the key design challenges and the innovative approaches used to overcome them.

Material Selection

Choosing the right material for a spring is crucial, as it directly affects the spring’s performance, durability, and cost. Common materials include music wire, and stainless steel, each with its unique properties.

• Music Wire ASTM A 228: Offers excellent elasticity and is commonly used in precision instruments and light mechanical applications.

• Stainless Steel ASTM A 313: Provides superior corrosion resistance, suitable for environments exposed to moisture or chemicals.

Material selection must consider factors such as environmental conditions, load requirements, and cost-effectiveness. Advanced materials like titanium or composite materials are also explored for specialized applications where weight and performance are critical.

Dimensional Constraints

Springs must often fit into compact spaces while maintaining their functionality. This requires precise control over dimensions, including wire diameter, coil diameter, and the number of active coils. The challenge lies in balancing these dimensions to achieve the desired spring rate and load capacity without compromising the spring's durability.

Using Acxess Spring's 3D CADs, designers can create detailed models of springs, allowing them to visualize and adjust dimensions before manufacturing. This reduces the risk of errors and ensures that the spring fits perfectly within the designated space.

Load Requirements

Springs must be designed to handle specific loads without permanent deformation or failure. This involves calculating the spring constant, stress distribution, and potential fatigue over repeated use. For example, compression springs in automotive suspensions must endure thousands of compression cycles while maintaining their performance.

Innovative simulation tools, like the Online Spring Force Tester provided by Acxess Spring, allow engineers to test spring designs under various load conditions virtually. By simulating real-world scenarios, designers can identify potential issues and optimize the spring's performance before physical testing.

Customization and Prototyping

Many applications require custom springs tailored to specific requirements. Creating custom compression springs, extension springs, torsion springs, or conical springs involves a detailed design process that can be time-consuming and costly. Each type of spring must meet precise specifications to function correctly in its intended application, whether it’s providing the necessary force, fitting into a limited space, or enduring specific environmental conditions. 

Acxess Spring offers advanced tools like 3D Blueprints and Online Spring Force Testers, which enable designers to quickly prototype and test custom springs. These tools facilitate the iterative design process, allowing for rapid adjustments and refinements based on testing results. With 3D Blueprints, designers can visualize their spring designs in detail, making it easier to identify potential issues and make necessary modifications before physical production. The Online Spring Force Testers provide accurate and immediate feedback on the spring's performance, ensuring that the final product meets all required specifications. This combination of tools accelerates the development cycle, reduces costs, and enhances the overall quality and reliability of custom springs. Whether for industrial machinery, automotive applications, medical devices, or consumer electronics, these innovative solutions from Acxess Spring help bring complex spring designs to life with greater precision and speed.

Optimize Your Spring Designs with Acxess Spring's Advanced Tools and Resources

Unlock the full potential of your spring designs with Acxess Spring's Instant Spring Quote! Whether you're working on custom compression springs, extension springs, torsion springs, or conical springs, our advanced tools and resources make the design process seamless and efficient. Get fast, accurate pricing for your specific requirements, and leverage our 3D Blueprints and Online Spring Force Testers to perfect your designs. Visit our website now to discover how Acxess Spring can help you bring your projects to life with precision and speed. Start your journey with our Instant Spring Quote tool today!